Introducción al agrupamiento K-Means
Updated on

K-Means es un popular algoritmo de aprendizaje no supervisado utilizado para el agrupamiento de datos. Es una técnica centrada en el centroide donde el objetivo es agrupar puntos de datos similares y separar los diferentes entre sí. Los algoritmos de agrupamiento se utilizan comúnmente en el aprendizaje automático para una variedad de aplicaciones como el perfilamiento de clientes, la segmentación de datos y la detección de valores atípicos.
¿Qué es el agrupamiento K-Means?
El agrupamiento K-Means es un método utilizado para dividir un conjunto de datos en K grupos diferentes, donde cada punto de datos pertenece al grupo con la media o centroide más cercano. Es una forma de encontrar similitudes entre los puntos de datos en un espacio de datos dado y agruparlos juntos.
¿Cómo funciona el agrupamiento K-Means?
El agrupamiento K-Means comienza inicializando aleatoriamente K centroides. Luego, asigna cada punto de datos al centroide más cercano según una métrica de distancia, como la Distancia Euclidiana. Se recalculan los centroides, y el proceso se repite hasta que los centroides ya no cambian significativamente o se cumple una condición predefinida.
Ventajas y desventajas del agrupamiento K-Means
Ventajas
- Simplicidad: K-Means es fácil de entender e implementar en Python.
- Eficiencia: K-Means es eficiente computacionalmente, lo que lo hace adecuado para conjuntos de datos grandes.
- Escalabilidad: K-Means puede adaptarse a conjuntos de datos grandes con numerosas variables.
Desventajas
- Número de grupos: El número de grupos (K) debe especificarse previamente.
- Sensibilidad a la inicialización: El resultado del algoritmo puede depender de la ubicación inicial de los centroides.
- Valores atípicos: K-Means es sensible a los valores atípicos, que pueden sesgar los centroides y los grupos resultantes.
Aplicaciones del agrupamiento K-Means
K-Means tiene una amplia variedad de aplicaciones, incluyendo:
- Perfilamiento de clientes: Las empresas pueden utilizar K-Means para segmentar su base de clientes y adaptar sus estrategias de marketing en consecuencia.
- Detección de valores atípicos: K-Means se puede utilizar para identificar anomalías o valores atípicos en conjuntos de datos, lo que es importante en campos como la detección de fraudes y la seguridad de redes.
- Reducción de dimensionalidad: K-Means se puede utilizar para reducir la dimensionalidad de los datos, lo que facilita su visualización e interpretación.
Implementación del agrupamiento K-Means en Python
La biblioteca sklearn de Python proporciona una forma sencilla de implementar K-Means. Aquí hay un ejemplo básico:
from sklearn.cluster import KMeans
## Ajuste el modelo a los datos
kmeans = KMeans(n_clusters=3)
kmeans.fit(datos)
## Obtener las asignaciones de grupo para cada punto de datos
labels = kmeans.labels_Puede manipular y preprocesar sus datos usando pandas. Si necesita una revisión de las operaciones de pandas, puede consultar Modin o PyGWalker (opens in a new tab).
¿Quieres crear rápida y fácilmente visualizaciones de datos en Python?
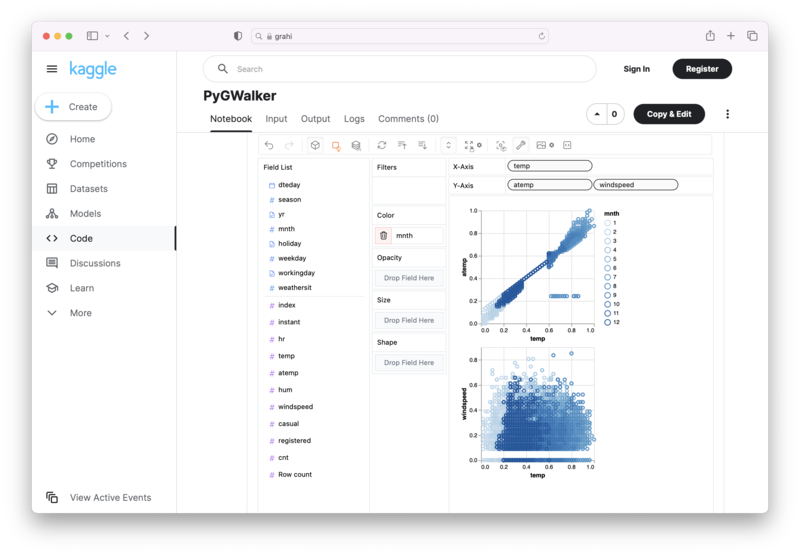
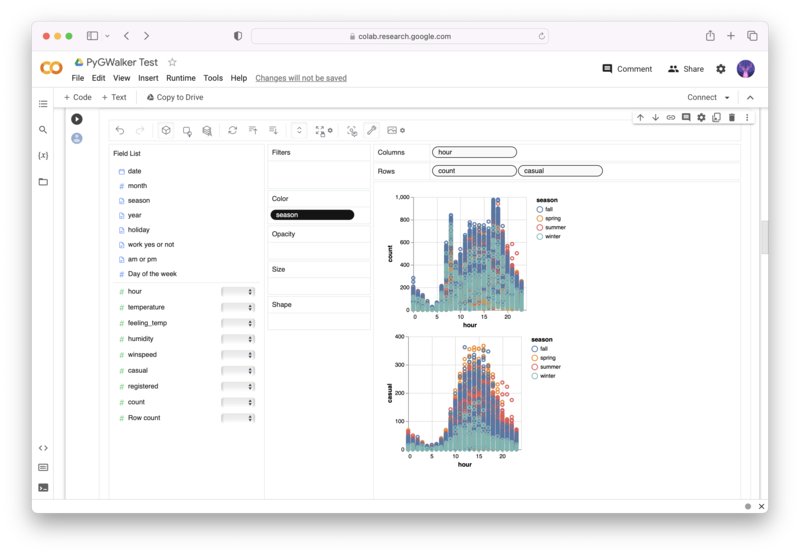
PyGWalker es un proyecto de Python de código abierto que puede ayudar a acelerar el flujo de trabajo de análisis y visualización de datos directamente en entornos basados en Jupyter Notebook.
PyGWalker (opens in a new tab) convierte su Pandas Dataframe (o Polars Dataframe) en una interfaz de usuario visual donde puede arrastrar y soltar variables para crear gráficos con facilidad. Simplemente use el siguiente código:
pip install pygwalker
import pygwalker as pyg
gwalker = pyg.walk(df)Puede ejecutar PyGWalker ahora mismo con estas notebooks en línea:
¡Y no olvide darnos una ⭐️ en GitHub!
Métricas de evaluación de clustering
Las métricas de evaluación nos ayudan a cuantificar la calidad de nuestros clusters. Aquí se muestran dos métricas comúnmente utilizadas:
- Score de Silueta: Mide qué tan similar es un objeto a su propio cluster en comparación con otros clusters.
- Inertia: Mide la suma total de cuadrados dentro del cluster. Un valor de inercia más bajo corresponde a una mejor cohesión del cluster.
Comparando K-Means con otros algoritmos de clustering
K-Means vs. Modelo de mezcla gaussiana (GMM)
Si bien tanto K-Means como el Model de mezcla gaussiana (GMM) son algoritmos de clustering, tienen diferencias fundamentales. K-Means es un método de clustering duro, lo que significa que un punto de datos pertenece por completo a un cluster. En contraste, GMM es un método de clustering suave que proporciona la probabilidad de que un punto de datos pertenezca a cada cluster.
K-Means vs. Clustering jerárquico
K-Means requiere especificar el número de clusters de antemano, mientras que el clustering jerárquico no lo necesita. El clustering jerárquico crea un árbol de clusters, que se puede visualizar e interpretar en diferentes niveles, proporcionando información más detallada sobre la estructura de los datos.
Casos de uso del clustering
El clustering tiene numerosos casos de uso en diferentes campos:
- Marketing: Para segmentación de clientes para comprender mejor los comportamientos de los clientes y adaptar las estrategias de marketing.
- Banca: Para detectar transacciones fraudulentas como outliers del comportamiento normal.
- Atención médica: Para la segmentación de pacientes basada en su historial médico para planes de tratamiento personalizados.
Elección del número de clusters
Seleccionar el número correcto de clusters es crucial en K-Means. Un método común es el Método del Codo, que consiste en graficar la variación explicada como una función del número de clusters y elegir el codo de la curva como el número de clusters a utilizar.
Detección de outliers utilizando K-Means
K-Means se puede utilizar para la detección de outliers. Los puntos de datos que se encuentran lejos del centroide de su cluster asignado se pueden considerar como outliers.
Ventajas del aprendizaje no supervisado en clustering
El aprendizaje no supervisado, como el clustering, tiene la ventaja de descubrir patrones y estructuras en los datos sin ningún conocimiento o entrenamiento previo. Esto lo hace particularmente útil cuando no tenemos datos etiquetados.
Conclusión
El clustering K-Means es una herramienta poderosa en la caja de herramientas del aprendizaje automático. Su simplicidad y versatilidad lo hacen una excelente opción para tareas que van desde la segmentación de clientes hasta la detección de outliers. Con una comprensión sólida de cómo funciona y sus posibles aplicaciones, estás bien equipado para empezar a utilizar el clustering K-Means en tus propios proyectos de ciencia de datos.