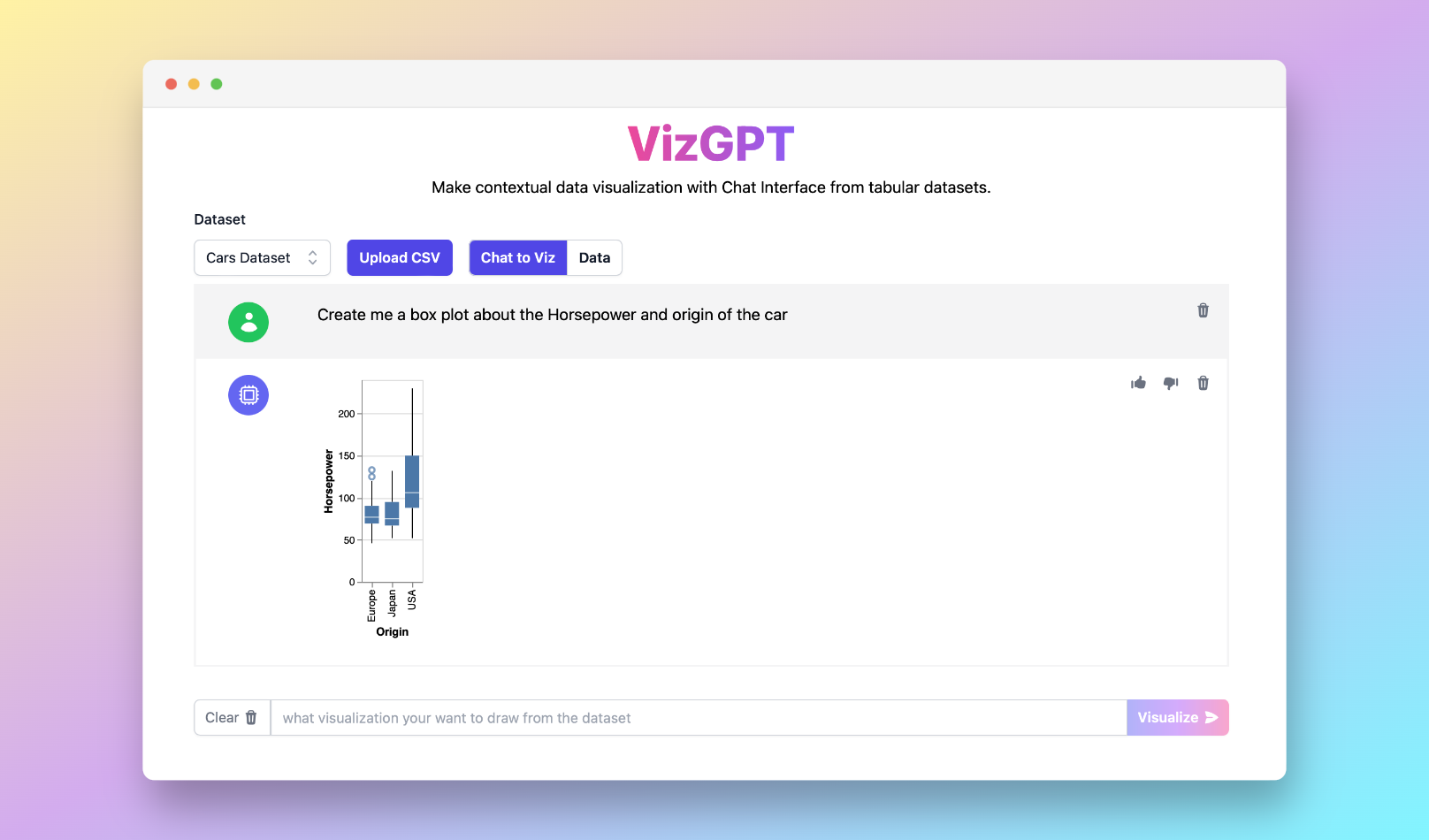
Mejor Calculadora de Diagrama de Caja en línea con VizGPT
¿Listo para empezar a crear tus propios diagramas de caja con VizGPT? Prueba esta indicación:
Crea un diagrama de caja a partir del conjunto de datos
¿Quieres subir un archivo CSV personalizado? Actualízate al Plan Kanaries Plus y obtén el paquete completo de aplicaciones (opens in a new tab) para manejar análisis de datos mucho más complicados.
Introducción
Los diagramas de caja, también conocidos como diagramas de caja y bigotes, son representaciones gráficas de datos que brindan información sobre la distribución y la variabilidad de los datos. Se utilizan ampliamente en el análisis estadístico y la visualización de datos. Esta guía tiene como objetivo desentrañar los fundamentos de los diagramas de caja, su objetivo en el análisis estadístico y el proceso de crearlos utilizando una calculadora de diagramas de caja.
Calculadora de Diagrama de Caja en línea: ¿Qué es?
Un diagrama de caja presenta el "resumen de los 5 números" de los datos: el mínimo, el primer cuartil (Q1), la mediana, el tercer cuartil (Q3) y el máximo. La caja misma muestra el rango intercuartílico (RI), que es el rango entre Q1 y Q3, representando el 50% intermedio de los datos. La línea dentro de la caja indica la mediana. Los "bigotes" a cada lado de la caja se extienden hasta los puntos de datos máximo y mínimo que no se consideran valores atípicos. Los valores atípicos, generalmente simbolizados como puntos o estrellas, representan puntos de datos significativamente distantes de los demás.
Los diagramas de caja son efectivos para comparar conjuntos de datos, identificar valores atípicos y comprender la dispersión y la asimetría de los datos. Sin embargo, a diferencia de los histogramas o los gráficos de densidad de núcleo, no muestran la forma exacta de la distribución ni la distribución de frecuencia subyacente.
Cálculo de Cuartiles Utilizando una Calculadora de Diagrama de Caja en línea
Calcular los cuartiles es un paso fundamental en la creación de un diagrama de caja. Los cuartiles dividen un conjunto de datos ordenado por rango en cuatro partes iguales. Q1 es el valor intermedio entre el número más pequeño y la mediana del conjunto de datos, Q2 es la mediana y Q3 es el valor intermedio entre la mediana y el número más grande.
Las calculadoras de diagramas de caja en línea, como Alcula, Omni Calculator o AtoZmath.com, brindan una forma sencilla de generar diagramas de caja a partir de datos sin procesar. Alternativamente, los usuarios pueden calcular manualmente los cuartiles y trazarlos utilizando Excel o calculadoras estadísticas como TI-84. Los modernos generadores de diagramas de caja ofrecen características como el cálculo del rango intercuartílico, la orientación horizontal y vertical, el cálculo de la media y la desviación estándar, e incluso la detección de valores atípicos para estadísticas descriptivas más avanzadas.
Interpretación de los Diagramas de Caja con una Calculadora de Diagrama de Caja en línea
Para comprender los diagramas de caja, es necesario conocer los componentes de los mismos. La caja representa el RI, proporcionando información sobre la dispersión de los datos. La línea mediana dentro de la caja indica la tendencia central de los datos. Los "bigotes" que se extienden desde la caja representan la variabilidad fuera de los cuartiles superior e inferior, mientras que los valores atípicos se marcan como puntos individuales.
La posición y longitud de estos componentes ofrecen información sobre la distribución de los datos. Por ejemplo, una caja más larga o "bigotes" más anchos sugieren mayor variabilidad en el conjunto de datos. La asimetría puede determinarse comparando la ubicación de la caja dentro de los "bigotes" o la posición de la mediana dentro de la caja.
Comparación e Importancia de la Calculadora de Diagrama de Caja en línea
Los diagramas de caja son útiles para comparar distribuciones entre diferentes conjuntos de datos. Al ver dos o más diagramas de caja uno al lado del otro, se pueden examinar las diferencias en la mediana, la dispersión y la simetría.
Los "bigotes" en un diagrama de caja tienen importancia estadística, indicando el rango dentro del cual se encuentran la mayoría de los datos y ayudando a identificar posibles valores atípicos.
Los diagramas de caja modificados, con su manejo específico de los valores atípicos, ofrecen una mayor robustez frente a interpretaciones sesgadas. Estos diagramas utilizan el RI para determinar qué constituye un valor atípico, brindando una visión más matizada de los datos.
Conclusión
En conclusión, los diagramas de caja son una herramienta poderosa para el análisis estadístico y la visualización de datos. Proporcionan una vista rápida de la distribución de los datos, la variabilidad y los valores atípicos. Las herramientas como las calculadoras de diagramas de caja y los generadores de diagramas de caja en línea simplifican el proceso de creación e interpretación de estos diagramas. Sin embargo, entender los principios detrás de los diagramas de caja, como los cuartiles y los rangos intercuartílicos, sigue siendo esencial para una interpretación precisa de los datos.
Preguntas frecuentes
¿Cuál es la importancia de los cuartiles en un diagrama de caja?
Los cuartiles dividen los datos en cuatro partes iguales, lo que permite la visualización de la mediana, el rango intercuartílico y la dispersión general de los datos en un diagrama de caja.
¿Cómo se pueden utilizar los diagramas de caja para la comparación?
Los diagramas de caja permiten la comparación lado a lado de diferentes conjuntos de datos, destacando las diferencias en la mediana, la dispersión, la simetría y los posibles valores atípicos.
¿Cuál es el papel de los valores atípicos en un diagrama de caja?
Los valores atípicos en un diagrama de caja son puntos de datos significativamente distantes de los demás. Son importantes para identificar anomalías en los datos.