Introdução ao Agrupamento K-Means

K-Means é um popular algoritmo de aprendizagem não supervisionada usado para agrupamento. É uma técnica centrada em centróides onde o objetivo é agrupar pontos de dados semelhantes e separar os dissimilares. Algoritmos de agrupamento são comumente usados em aprendizado de máquina para uma variedade de aplicações, como perfil de clientes, segmentação de dados e detecção de pontos anômalos.
O Que é Agrupamento K-Means?
Agrupamento K-Means é um método usado para particionar um conjunto de dados em K diferentes grupos, onde cada ponto de dados pertence ao grupo com a média ou centroid mais próxima. É uma forma de encontrar similaridades entre pontos de dados em um determinado espaço de dados e agrupá-los.
Como Funciona o Agrupamento K-Means?
O agrupamento K-Means começa inicializando aleatoriamente K centroides. Em seguida, atribui cada ponto de dados ao centroide mais próximo com base em uma métrica de distância, como a Distância Euclidiana. Os centroides são recalculados e o processo é repetido até que os centroides não mudem significativamente ou uma condição predefinida seja atendida.
Vantagens e Desvantagens do Agrupamento K-Means
Vantagens
- Simplicidade: O K-Means é fácil de entender e implementar em Python.
- Eficiência: O K-Means é computacionalmente eficiente, o que o torna adequado para grandes conjuntos de dados.
- Escalabilidade: O K-Means pode escalar para lidar com grandes conjuntos de dados com inúmeras variáveis.
Desvantagens
- Número de Grupos: O número de grupos (K) precisa ser especificado antecipadamente.
- Sensibilidade à Inicialização: O resultado do algoritmo pode depender da localização inicial dos centroides.
- Pontos Anômalos: O K-Means é sensível a pontos anômalos, o que pode distorcer os centroides e os grupos resultantes.
Aplicações do Agrupamento K-Means
O K-Means tem uma ampla variedade de aplicações, incluindo:
- Perfil de Clientes: Empresas podem usar o K-Means para segmentar sua base de clientes e ajustar suas estratégias de marketing de acordo.
- Detecção de Pontos Anômalos: O K-Means pode ser usado para identificar anomalias ou outliers em conjuntos de dados, o que é importante em campos como detecção de fraudes e segurança de rede.
- Redução da Dimensionalidade: O K-Means pode ser usado para reduzir a dimensionalidade dos dados, facilitando a visualização e a interpretação.
Implementação do Agrupamento K-Means em Python
A biblioteca sklearn do Python fornece uma maneira simples de implementar o K-Means. Aqui está um exemplo básico:
from sklearn.cluster import KMeans
## Ajuste o modelo aos dados
kmeans = KMeans(n_clusters=3)
kmeans.fit(dados)
## Obtenha as atribuições de grupo para cada ponto de dados
labels = kmeans.labels_Você pode manipular e pré-processar seus dados usando pandas. Se precisar de uma atualização sobre as operações do pandas, pode conferir Modin ou PyGWalker (opens in a new tab).
Quer criar visualizações de dados rapidamente em Python?
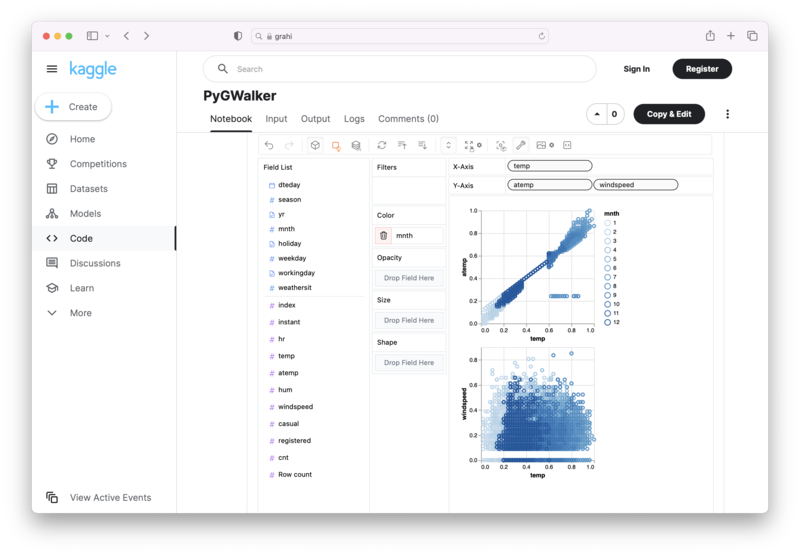
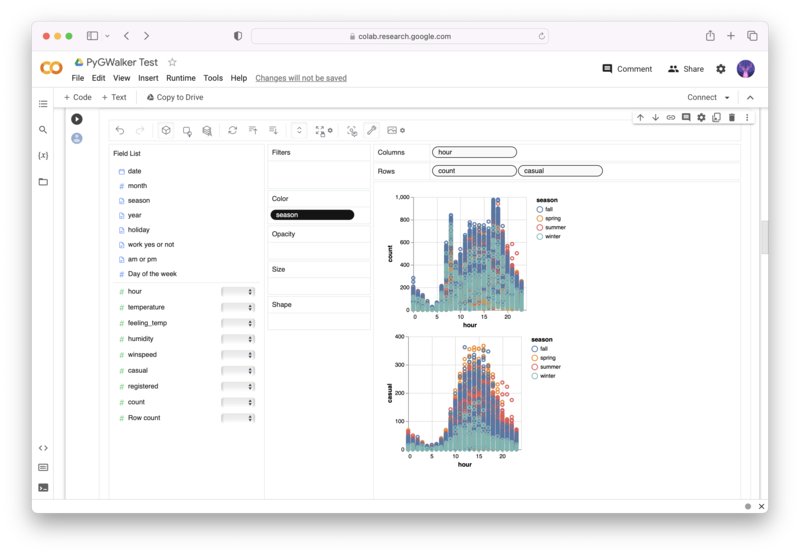
PyGWalker é um projeto de código aberto em Python que pode ajudar a acelerar o fluxo de análise de dados e visualização diretamente em ambientes baseados em Jupyter Notebook.
PyGWalker (opens in a new tab) transforma seu dataframe pandas (ou dataframe Polars) em uma interface visual na qual você pode arrastar e soltar variáveis para criar gráficos com facilidade. Basta usar o seguinte código:
pip install pygwalker
import pygwalker as pyg
gwalker = pyg.walk(df)Você pode executar o PyGWalker agora mesmo com esses notebooks online:
E não se esqueça de dar uma ⭐️ no GitHub!
Métricas de Avaliação de Clusterização
Métricas de avaliação nos ajudam a quantificar a qualidade dos nossos clusters. Aqui estão duas métricas comumente usadas:
- Score de Silhueta: Mede o quão similar um objeto é ao seu próprio cluster em comparação com outros clusters.
- Inércia: Mede a soma total dos quadrados dentro do cluster. Um valor de inércia mais baixo corresponde a maior coerência do cluster.
Comparando K-Means com Outros Algoritmos de Clusterização
K-Means vs. Gaussian Mixture Model (GMM)
Enquanto tanto K-Means quanto o Modelo de Mistura Gaussiano (GMM) são algoritmos de clusterização, eles possuem diferenças fundamentais. K-Means é um método de clusterização hard, ou seja, um ponto de dados pertence completamente a um cluster. Em contraste, GMM é um método de clusterização soft que fornece a probabilidade de um ponto de dados pertencer a cada cluster.
K-Means vs. Clusterização Hierárquica
K-Means requer a especificação do número de clusters a priori, enquanto a clusterização hierárquica não precisa disso. A clusterização hierárquica cria uma árvore de clusters, que pode ser visualizada e interpretada em diferentes níveis, proporcionando informações mais granulares sobre a estrutura dos dados.
Casos de Uso de Clusterização
Clusterização tem inúmeros casos de uso em diferentes áreas:
- Marketing: Para segmentação de clientes a fim de entender melhor o comportamento dos clientes e adaptar as estratégias de marketing.
- Bancário: Para detecção de transações fraudulentas como pontos fora da curva do comportamento normal.
- Assistência médica: Para segmentação de pacientes com base em seus históricos médicos para planos de tratamento personalizados.
Escolha do Número de Clusters
A escolha correta do número de clusters é crucial no K-Means. Um método comum é o Método do Cotovelo, que envolve traçar a variação explicada como uma função do número de clusters e escolher o cotovelo da curva como o número de clusters a ser usado.
Detecção de Outliers usando K-Means
K-Means pode ser usado para detecção de outliers. Os pontos de dados que estão longe do centróide do seu cluster atribuído podem ser considerados como outliers.
Vantagens do Aprendizado Não Supervisionado em Clustering
O aprendizado não supervisionado, como o clustering, tem a vantagem de descobrir padrões e estruturas em dados sem qualquer conhecimento prévio ou treinamento. Isso o torna particularmente útil quando não temos dados rotulados.
Conclusão
O clustering K-Means é uma ferramenta poderosa na caixa de ferramentas de aprendizado de máquina. Sua simplicidade e versatilidade o tornam uma excelente escolha para tarefas que vão desde segmentação de clientes até a detecção de outliers. Com uma compreensão sólida de como ele funciona e suas aplicações potenciais, você está bem equipado para começar a usar o clustering K-Means em seus próprios projetos de ciência de dados.