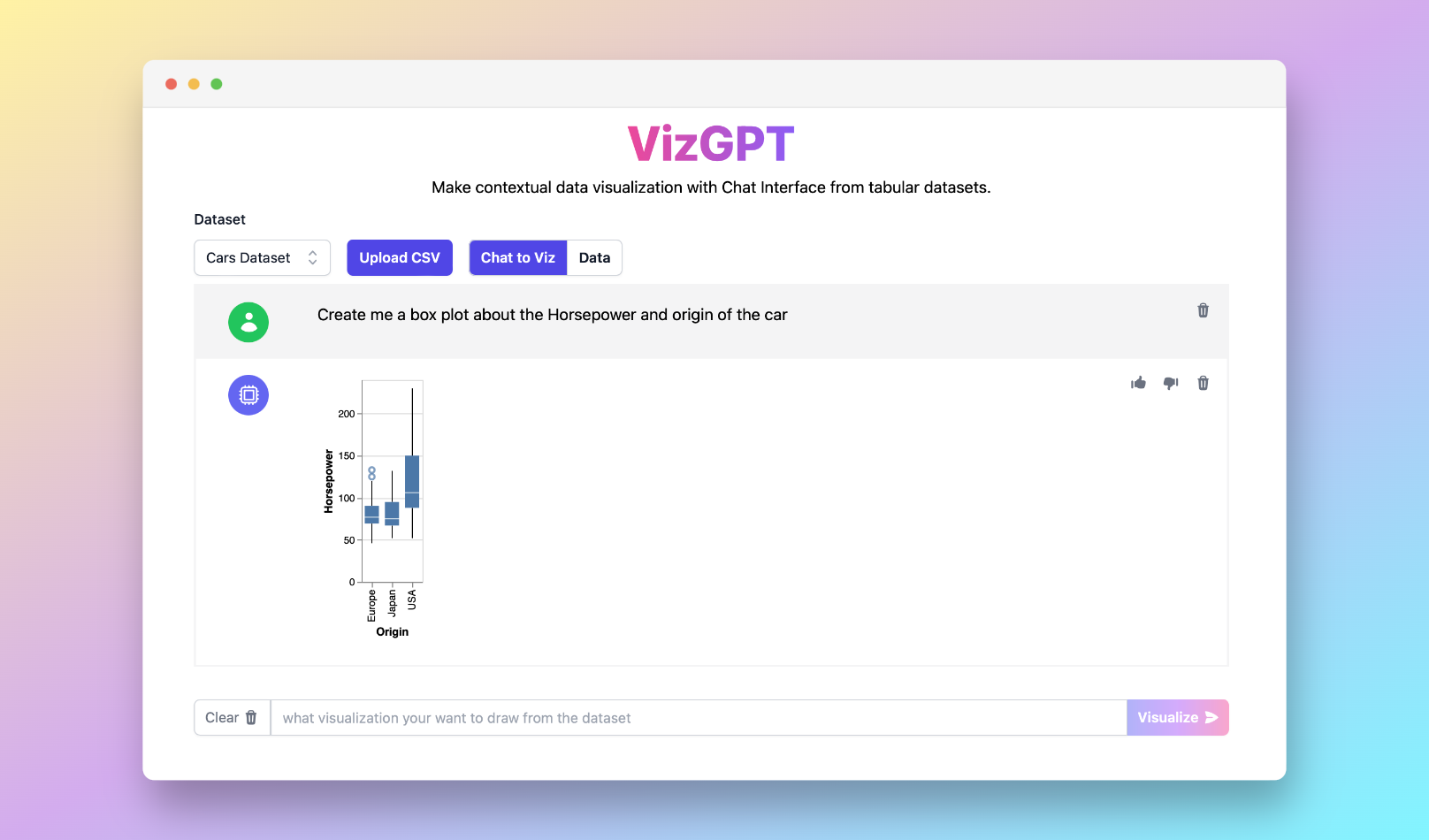
Meilleure calculatrice de boîtes à moustaches en ligne avec VizGPT
Prêt à commencer à créer vos propres boîtes à moustaches avec VizGPT ? Essayez cette invite :
Créez une boîte à moustaches à partir de l'ensemble de données
Vous souhaitez télécharger un fichier CSV personnalisé ? Passez au plan Kanaries Plus, vous pourrez obtenir le package complet d'applications (opens in a new tab) pour gérer des analyses de données beaucoup plus complexes !
Introduction
Les boîtes à moustaches, également appelées diagrammes à moustaches ou diagrammes en boîte, sont des représentations graphiques de données qui fournissent des informations sur la répartition et la variabilité des données. Elles sont largement utilisées dans l'analyse statistique et la visualisation des données. Ce guide vise à dévoiler les fondamentaux des boîtes à moustaches, leur objectif dans l'analyse statistique et le processus de création à l'aide d'une calculatrice de boîtes à moustaches.
Calculatrice de boîtes à moustaches en ligne : Qu'est-ce que c'est ?
Un diagramme en boîte présente le "résumé en 5 nombres" des données : le minimum, le premier quartile (Q1), la médiane, le troisième quartile (Q3) et le maximum. La boîte elle-même affiche l'intervalle interquartile (IIQ), qui est la plage entre Q1 et Q3, représentant les 50 % centraux des données. La ligne à l'intérieur de la boîte indique la médiane. Les "moustaches" de chaque côté de la boîte s'étendent jusqu'aux points de données maximum et minimum qui ne sont pas considérés comme des valeurs aberrantes. Les valeurs aberrantes, généralement symbolisées par des points ou des étoiles, représentent des points de données significativement éloignés des autres.
Les boîtes à moustaches sont efficaces pour comparer des ensembles de données, identifier des valeurs aberrantes et comprendre la dispersion et la symétrie des données. Cependant, contrairement aux histogrammes ou aux graphiques de densité de noyau, elles ne représentent pas précisément la forme de la distribution ou la distribution de fréquences sous-jacente.
Calcul des quartiles à l'aide d'une calculatrice de boîtes à moustaches en ligne
Le calcul des quartiles est une étape fondamentale dans la création d'un diagramme en boîte. Les quartiles divisent un ensemble de données triées en quatre parties égales. Q1 est la valeur médiane entre le nombre le plus petit et la médiane de l'ensemble de données, Q2 est la médiane et Q3 est la valeur médiane entre la médiane et le nombre le plus élevé.
Les calculatrices en ligne de diagrammes en boîte, telles que Alcula, Omni Calculator ou AtoZmath.com, permettent de générer facilement des diagrammes en boîte à partir de données brutes. Alternativement, les utilisateurs peuvent calculer manuellement les quartiles et tracer le diagramme à l'aide d'Excel ou de calculatrices statistiques comme le TI-84. Les outils modernes de création de diagrammes en boîte offrent des fonctionnalités telles que le calcul de l'intervalle interquartile, l'orientation horizontale et verticale, le calcul de la moyenne et de l'écart type, et même la détection des valeurs aberrantes pour des statistiques descriptives plus avancées.
Interprétation des boîtes à moustaches à l'aide d'une calculatrice de boîtes à moustaches en ligne
Comprendre les boîtes à moustaches nécessite la connaissance de leurs composants. La boîte représente l'IIQ, offrant un aperçu de la dispersion des données. La ligne médiane à l'intérieur de la boîte indique la tendance centrale des données. Les "moustaches" qui s'étendent à partir de la boîte représentent la variabilité en dehors des quartiles supérieur et inférieur, tandis que les valeurs aberrantes sont marquées comme des points individuels.
La position et la longueur de ces composantes fournissent des informations sur la répartition des données. Par exemple, une boîte plus longue ou des "moustaches" plus larges suggèrent une plus grande variabilité dans l'ensemble de données. La symétrie peut être déterminée en comparant la position de la boîte par rapport aux "moustaches" ou la position de la médiane par rapport à la boîte.
Comparaison et importance d'une calculatrice de boîtes à moustaches en ligne
Les boîtes à moustaches sont utiles pour comparer des distributions entre différents ensembles de données. Lorsque l'on regarde deux ou plusieurs boîtes à moustaches côte à côte, on peut examiner les différences de médiane, de dispersion et de symétrie.
Les "moustaches" dans un diagramme en boîte ont une signification statistique, indiquant la plage dans laquelle la plupart des données se trouvent et contribuant à l'identification d'éventuelles valeurs aberrantes.
Les diagrammes en boîte modifiés, avec leur gestion spécifique des valeurs aberrantes, offrent une robustesse supplémentaire contre les interprétations biaisées. Ces diagrammes utilisent l'IIQ pour déterminer ce qui constitue une valeur aberrante, offrant une vue plus nuancée des données.
Conclusion
En conclusion, les boîtes à moustaches sont un outil puissant pour l'analyse statistique et la visualisation des données. Elles permettent d'avoir une vue rapide de la répartition des données, de leur variabilité et des valeurs aberrantes. Les outils tels que les calculatrices de boîtes à moustaches et les créateurs de boîtes à moustaches en ligne simplifient le processus de création et d'interprétation de ces diagrammes. Cependant, il est essentiel de comprendre les principes des boîtes à moustaches, tels que les quartiles et les intervalles interquartiles, pour une interprétation précise des données.
FAQ
Quelle est l'importance des quartiles dans un diagramme en boîte ?
Les quartiles divisent les données en quatre parties égales, permettant la visualisation de la médiane, de l'intervalle interquartile et de la répartition générale des données dans un diagramme en boîte.
Comment peut-on utiliser les diagrammes en boîte pour la comparaison ?
Les diagrammes en boîte permettent de comparer côte à côte différents ensembles de données, mettant en évidence les différences de médiane, de dispersion, de symétrie et de valeurs aberrantes potentielles.
Quel est le rôle des valeurs aberrantes dans un diagramme en boîte ?
Les valeurs aberrantes dans un diagramme en boîte sont des points de données significativement éloignés des autres. Elles sont importantes pour identifier les anomalies dans les données.