Equação de Regressão Logística em R: Entendendo a Fórmula com Exemplos
Updated on
A regressão logística é uma das técnicas estatísticas mais populares usadas em aprendizado de máquina para problemas de classificação binária. Ela usa uma função logística para modelar a relação entre uma variável dependente e uma ou mais variáveis independentes. O objetivo da regressão logística é encontrar a melhor relação entre as características de entrada e a variável de saída. Neste artigo, discutiremos a equação de regressão logística com exemplos em R.
Quer criar rapidamente a Visualização de Dados a partir de um Dataframe Python Pandas sem código?
PyGWalker é uma biblioteca Python para Análise Exploratória de Dados com Visualização. PyGWalker (opens in a new tab) pode simplificar sua análise de dados e fluxo de trabalho de visualização de dados no Jupyter Notebook, transformando seu dataframe pandas (e dataframe polars) em uma Interface de Usuário de estilo Tableau para exploração visual.
Equação de Regressão Logística
A equação de regressão logística pode ser definida da seguinte forma:
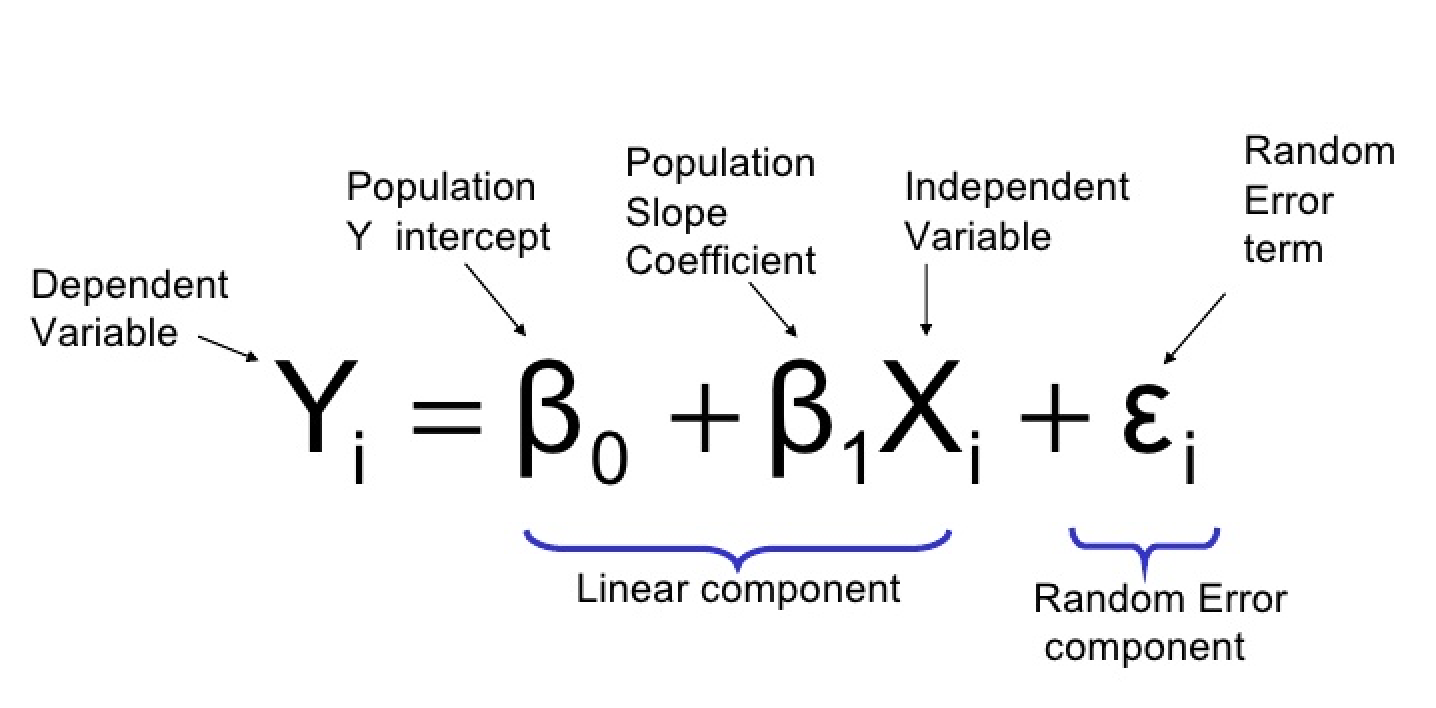
onde:
- Y: a variável dependente ou variável de resposta (binária)
- X1, X2, ..., Xp: variáveis independentes ou preditoras
- β0, β1, β2, ..., βp: coeficientes beta ou parâmetros do modelo
O modelo de regressão logística estima os valores dos coeficientes beta. Os coeficientes beta representam a mudança nos log-odds da variável dependente quando a variável independente correspondente muda em uma unidade. A função logística (também chamada de função sigmoide) então transforma os log-odds em probabilidades entre 0 e 1.
Aplicando a Regressão Logística em R
Nesta seção, usaremos a função glm() em R para construir e treinar um modelo de regressão logística em um conjunto de dados de exemplo. Usaremos o conjunto de dados hr_analytics do pacote RSample.
Carregando os Dados
Primeiro, carregamos o pacote e o conjunto de dados necessários:
library(RSample)
data(hr_analytics)O conjunto de dados hr_analytics contém informações sobre os funcionários de uma determinada empresa, incluindo idade, gênero, nível de educação, departamento e se eles deixaram a empresa ou não.
Preparando os Dados
Convertemos a variável alvo left_company em uma variável binária:
hr_analytics$left_company <- ifelse(hr_analytics$left_company == "Yes", 1, 0)Em seguida, dividimos o conjunto de dados em conjuntos de treinamento e teste:
set.seed(123)
split <- initial_split(hr_analytics, prop = 0.7)
train <- training(split)
test <- testing(split)Construindo o Modelo
Ajustamos um modelo de regressão logística usando a função glm():
logistic_model <- glm(left_company ~ ., data = train, family = "binomial")Neste exemplo, usamos todas as variáveis independentes disponíveis (idade, gênero, educação, departamento) para prever a variável dependente (left_company). O argumento family especifica o tipo de modelo que queremos ajustar. Como estamos lidando com um problema de classificação binária, especificamos "binomial" como a família.
Avaliando o Modelo
Para avaliar o desempenho do modelo, usamos a função summary():
summary(logistic_model)Output:
Call:
glm(formula = left_company ~ ., family = "binomial", data = train)
Deviance Residuals:
Min 1Q Median 3Q Max
-2.389 -0.640 -0.378 0.665 2.866
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -0.721620 0.208390 -3.462 0.000534 ***
age -0.008328 0.004781 -1.742 0.081288 .
genderMale 0.568869 0.086785 6.553 5.89e-11 ***
educationHigh School 0.603068 0.132046 4.567 4.99e-06 ***
educationMaster's -0.175406 0.156069 -1.123 0.261918
departmentHR 1.989789 0.171596 11.594 < 2e-16 ***
departmentIT 0.906366 0.141395 6.414 1.39e-10 ***
departmentSales 1.393794 0.177948 7.822 5.12e-15 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 6589.7 on 4799 degrees of freedom
Residual deviance: 5878.5 on 4792 degrees of freedom
AIC: 5894.5
Number of Fisher Scoring iterations: 5A saída mostra os coeficientes do modelo (coeficientes beta), seus erros padrão, valor z e valor p. Podemos interpretar os coeficientes da seguinte forma:
- Os coeficientes com um valor p significativo (p < 0,05) são estatisticamente significativos e têm um impacto significativo no resultado. Neste caso, idade, gênero, educação e departamento são preditores significativos se um funcionário deixa a empresa ou não.
- Os coeficientes com um valor p não significativo (p > 0,05) não são estatisticamente significativos e não têm impacto significativo no resultado. Neste caso, o nível de educação (Mestrado) não é um preditor significativo.
Fazendo Previsões
Para fazer previsões em novos dados, usamos a função predict():
predictions <- predict(logistic_model, newdata = test, type = "response")O argumento newdata especifica os novos dados nos quais queremos fazer previsões. O argumento type especifica o tipo de saída que queremos. Como estamos lidando com classificação binária, especificamos "response" como o tipo.
Avaliando as Previsões
Por fim, avaliamos as previsões usando a matriz de confusão:
table(Predicted = ifelse(predictions > 0.5, 1, 0), Actual = test$left_company)Output:
Actual
Predicted 0 1
0 1941 334
1 206 419A matriz de confusão mostra o número de verdadeiros positivos, falsos positivos, verdadeiros negativos e falsos negativos. Podemos usar esses valores para calcular métricas de desempenho como precisão, recall e pontuação F1.
Conclusão
Neste artigo, discutimos a equação de regressão logística e como ela é usada para modelar a relação entre variáveis independentes e uma variável binária dependente. Também demonstramos como usar a função glm() em R para construir, treinar e avaliar um modelo de regressão logística em um conjunto de dados de exemplo. A regressão logística é uma técnica poderosa para problemas de classificação binária e é amplamente utilizada em aprendizado de máquina.