Skip to content

lab2.dev is launched! Build python web apps with plain English, no code required.

Équation de régression logistique en R : Comprendre la formule avec des exemples

Rajiv Chandra
Name
Rajiv Chandra

Updated on

La régression logistique est l'une des techniques statistiques les plus populaires utilisées en apprentissage automatique pour les problèmes de classification binaire. Elle utilise une fonction logistique pour modéliser la relation entre une variable dépendante et une ou plusieurs variables indépendantes. L'objectif de la régression logistique est de trouver la meilleure relation entre les caractéristiques d'entrée et la variable de sortie. Dans cet article, nous discuterons de l'équation de régression logistique avec des exemples en R.

Vous voulez créer rapidement une visualisation de données à partir d'un dataframe Python Pandas sans code ?

PyGWalker est une bibliothèque Python pour l'analyse exploratoire de données avec visualisation. PyGWalker (opens in a new tab) peut simplifier votre flux de travail d'analyse de données et de visualisation de données dans Jupyter Notebook en transformant votre dataframe pandas (et dataframe polars) en une interface utilisateur de style Tableau pour l'exploration visuelle.

PyGWalker pour la visualisation de données (opens in a new tab)

Équation de régression logistique

L'équation de régression logistique peut être définie comme suit :

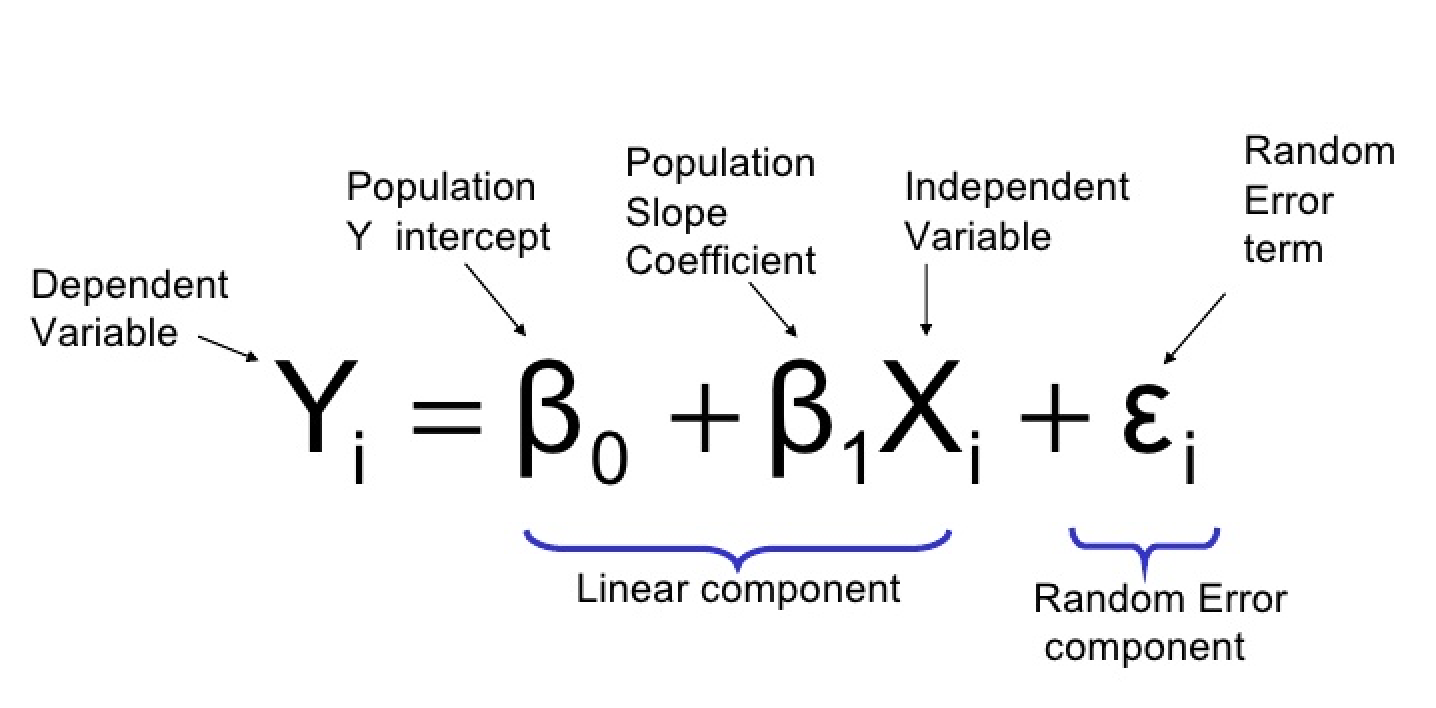
Régression logistique

où :

  • Y : la variable dépendante ou variable de réponse (binaire)
  • X1, X2, …, Xp : variables indépendantes ou prédicteurs
  • β0, β1, β2, …, βp : coefficients bêta ou paramètres du modèle

Le modèle de régression logistique estime les valeurs des coefficients bêta. Les coefficients bêta représentent le changement dans les logarithmes des cotes de la variable dépendante lorsque la variable indépendante correspondante change d'une unité. La fonction logistique (également appelée fonction sigmoïde) transforme ensuite les logarithmes des cotes en probabilités entre 0 et 1.

Application de la régression logistique en R

Dans cette section, nous utiliserons la fonction glm() en R pour construire et entraîner un modèle de régression logistique sur un jeu de données d'exemple. Nous utiliserons le jeu de données hr_analytics du package RSample.

Chargement des données

Tout d'abord, nous chargeons le package et le jeu de données requis :

library(RSample)
data(hr_analytics)

Le jeu de données hr_analytics contient des informations sur les employés d'une certaine entreprise, notamment leur âge, leur sexe, leur niveau d'éducation, leur département et s'ils ont quitté l'entreprise ou non.

Préparation des données

Nous convertissons la variable cible left_company en une variable binaire :

hr_analytics$left_company <- ifelse(hr_analytics$left_company == "Oui", 1, 0)

Ensuite, nous divisons le jeu de données en ensembles d'entraînement et de test :

set.seed(123)
split <- initial_split(hr_analytics, prop = 0.7)
train <- training(split)
test <- testing(split)

Construction du modèle

Nous ajustons un modèle de régression logistique à l'aide de la fonction glm() :

logistic_model <- glm(left_company ~ ., data = train, family = "binomial")

Dans cet exemple, nous utilisons toutes les variables indépendantes disponibles (âge, sexe, éducation, département) pour prédire la variable dépendante (left_company). L'argument family spécifie le type de modèle que nous voulons ajuster. Étant donné que nous traitons d'un problème de classification binaire, nous spécifions "binomial" comme famille.

Évaluation du modèle

Pour évaluer les performances du modèle, nous utilisons la fonction summary() :

summary(logistic_model)

Sortie :

Appel :
glm(formula = left_company ~ ., family = "binomial", data = train)

Résidus de déviance : 
   Min      1Q  Médiane      3Q     Max  
-2.389  -0.640  -0.378   0.665   2.866  

Coefficients :
                     Estimate Std. Error z value Pr(>|z|)    
(Intercept)         -0.721620   0.208390  -3.462 0.000534 ***
age                 -0.008328   0.004781  -1.742 0.081288 .  
genderMale           0.568869   0.086785   6.553 5.89e-11 ***
educationHigh School 0.603068   0.132046   4.567 4.99e-06 ***
educationMaster's   -0.175406   0.156069  -1.123 0.261918    
departmentHR         1.989789   0.171596  11.594  < 2e-16 ***
departmentIT         0.906366   0.141395   6.414 1.39e-10 ***
departmentSales      1.393794   0.177948   7.822 5.12e-15 ***
---
Codes de signification :  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 6589.7  on 4799  degrees of freedom
Residual deviance: 5878.5  on 4792  degrees of freedom
AIC: 5894.5

Number of Fisher Scoring iterations: 5

La sortie affiche les coefficients du modèle (coefficients bêta), leurs erreurs standard, la valeur z et la valeur p. Nous pouvons interpréter les coefficients comme suit :

  • Les coefficients ayant une valeur p significative (p < 0.05) sont statistiquement significatifs et ont un impact significatif sur le résultat. Dans ce cas, l'âge, le sexe, l'éducation et le département sont des prédicteurs significatifs de la décision d'un employé de quitter ou non l'entreprise.
  • Les coefficients ayant une valeur p non significative (p > 0.05) ne sont pas statistiquement significatifs et n'ont pas d'impact significatif sur le résultat. Dans ce cas, le niveau d'éducation (Master's) n'est pas un prédicteur significatif.

Prédictions

Pour effectuer des prédictions sur de nouvelles données, nous utilisons la fonction predict() :

predictions <- predict(logistic_model, newdata = test, type = "response")

L'argument newdata spécifie les nouvelles données sur lesquelles nous souhaitons effectuer des prédictions. L'argument type spécifie le type de sortie souhaité. Étant donné que nous traitons une classification binaire, nous spécifions "response" comme type.

Évaluation des prédictions

Enfin, nous évaluons les prédictions à l'aide de la matrice de confusion :

table(Predicted = ifelse(predictions > 0.5, 1, 0), Actual = test$left_company)

Sortie : Voici la traduction en français de ce fichier markdown sans traduire le code intégré :

         Actual
Predicted    0    1
        0 1941  334
        1  206  419

La matrice de confusion montre le nombre de vrais positifs, de faux positifs, de vrais négatifs et de faux négatifs. Nous pouvons utiliser ces valeurs pour calculer des métriques de performance telles que la précision, le rappel et le score F1.

Conclusion

Dans cet article, nous avons discuté de l'équation de régression logistique et de son utilisation pour modéliser la relation entre les variables indépendantes et une variable binaire dépendante. Nous avons également montré comment utiliser la fonction glm() en R pour construire, entraîner et évaluer un modèle de régression logistique sur un ensemble de données d'échantillon. La régression logistique est une technique puissante pour les problèmes de classification binaire et est largement utilisée en apprentissage automatique.