Skip to content

lab2.dev is launched! Build python web apps with plain English, no code required.

Logistische Regression Gleichung in R: Verständnis der Formel mit Beispielen

Rajiv Chandra
Name
Rajiv Chandra

Updated on

Die logistische Regression ist eine der beliebtesten statistischen Techniken, die in der maschinellen Lernforschung für binäre Klassifikationsprobleme verwendet wird. Sie verwendet eine logistische Funktion, um die Beziehung zwischen einer abhängigen Variable und einer oder mehreren unabhängigen Variablen zu modellieren. Das Ziel der logistischen Regression besteht darin, die beste Beziehung zwischen den Eingabefeatures und der Ausgabevariable zu finden. In diesem Artikel werden wir die logistische Regression Gleichung mit Beispielen in R diskutieren.

Möchten Sie schnell Datenvisualisierung aus Python Pandas Dataframe ohne Code erstellen?

PyGWalker ist eine Python-Bibliothek für explorative Datenanalyse mit Visualisierung. PyGWalker (opens in a new tab) kann Ihren Workflow der Datenanalyse und der Datenvisualisierung in Jupyter Notebook vereinfachen, indem es Ihr Pandas Dataframe (und Polars Dataframe) in eine benutzerfreundliche Oberfläche im Stil von Tableau verwandelt, mit der Sie visuelle Exploration durchführen können.

PyGWalker für Datenvisualisierung (opens in a new tab)

Logistische Regression Gleichung

Die logistische Regression Gleichung kann wie folgt definiert werden:

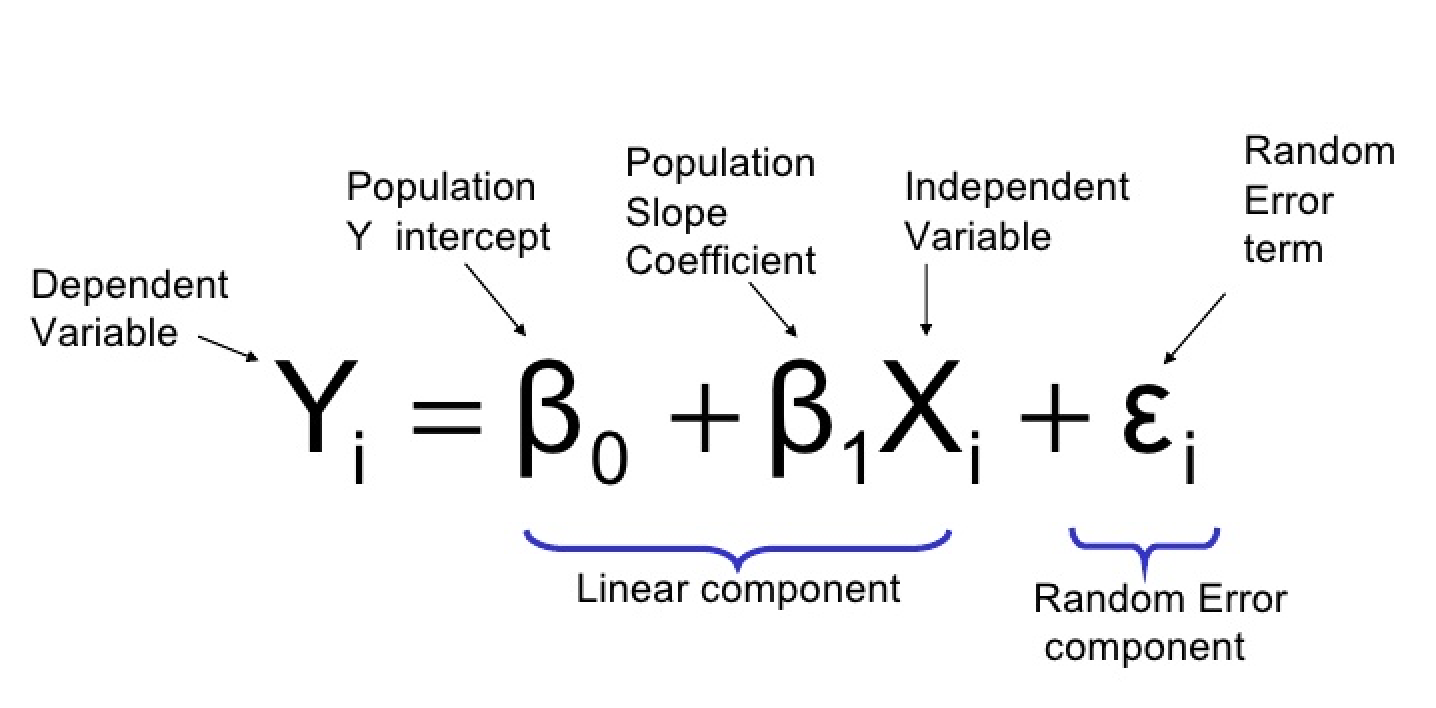
Logistische Regression

wobei:

  • Y: die abhängige Variable oder die Response-Variable (binär)
  • X1, X2, …, Xp: unabhängige Variablen oder Prädiktoren
  • β0, β1, β2, …, βp: Beta-Koeffizienten oder Modellparameter

Das logistische Regressionsmodell schätzt die Werte der Beta-Koeffizienten. Die Beta-Koeffizienten stellen die Änderung der Log-Odds der abhängigen Variable dar, wenn sich die entsprechende unabhängige Variable um eine Einheit ändert. Die logistische Funktion (auch Sigmoid-Funktion genannt) transformiert dann die Log-Odds in Wahrscheinlichkeiten zwischen 0 und 1.

Anwendung der logistischen Regression in R

In diesem Abschnitt verwenden wir die glm() Funktion in R, um ein logistisches Regressionsmodell auf einem Beispieldatensatz zu erstellen und zu trainieren. Wir verwenden den Datensatz hr_analytics aus dem Paket RSample.

Laden der Daten

Zuerst laden wir das erforderliche Paket und den Datensatz:

library(RSample)
data(hr_analytics)

Der hr_analytics Datensatz enthält Informationen über Mitarbeiter eines bestimmten Unternehmens, einschließlich ihres Alters, Geschlechts, Bildungsstands, Abteilungszugehörigkeit und ob sie das Unternehmen verlassen haben oder nicht.

Daten vorbereiten

Wir wandeln die Zielvariable left_company in eine binäre Variable um:

hr_analytics$left_company <- ifelse(hr_analytics$left_company == "Yes", 1, 0)

Dann teilen wir den Datensatz in Trainings- und Testsets auf:

set.seed(123)
split <- initial_split(hr_analytics, prop = 0.7)
train <- training(split)
test <- testing(split)

Modell erstellen

Wir passen ein logistisches Regressionsmodell mit der glm() Funktion an:

logistic_model <- glm(left_company ~ ., data = train, family = "binomial")

In diesem Beispiel verwenden wir alle verfügbaren unabhängigen Variablen (Alter, Geschlecht, Bildung, Abteilung) zur Vorhersage der abhängigen Variable (left_company). Das family Argument gibt den Modelltyp an, den wir anpassen möchten. Da wir es mit einem binären Klassifikationsproblem zu tun haben, geben wir "binomial" als Familie an.

Bewertung des Modells

Um die Leistung des Modells zu bewerten, verwenden wir die summary() Funktion:

summary(logistic_model)

Ausgabe:

Call:
glm(formula = left_company ~ ., family = "binomial", data = train)

Deviance Residuals: 
   Min      1Q  Median      3Q     Max  
-2.389  -0.640  -0.378   0.665   2.866  

Coefficients:
                     Estimate Std. Error z value Pr(>|z|)    
(Intercept)         -0.721620   0.208390  -3.462 0.000534 ***
age                 -0.008328   0.004781  -1.742 0.081288 .  
genderMale           0.568869   0.086785   6.553 5.89e-11 ***
educationHigh School 0.603068   0.132046   4.567 4.99e-06 ***
educationMaster's   -0.175406   0.156069  -1.123 0.261918    
departmentHR         1.989789   0.171596  11.594  < 2e-16 ***
departmentIT         0.906366   0.141395   6.414 1.39e-10 ***
departmentSales      1.393794   0.177948   7.822 5.12e-15 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 6589.7  on 4799  degrees of freedom
Residual deviance: 5878.5  on 4792  degrees of freedom
AIC: 5894.5

Number of Fisher Scoring iterations: 5

Die Ausgabe zeigt die Koeffizienten des Modells (Beta-Koeffizienten), ihre Standardfehler, z-Wert und p-Wert. Wir können die Koeffizienten wie folgt interpretieren:

  • Die Koeffizienten mit einem signifikanten p-Wert (p < 0,05) sind statistisch signifikant und haben einen signifikanten Einfluss auf das Ergebnis. In diesem Fall sind Alter, Geschlecht, Bildung und Abteilung signifikante Prädiktoren dafür, ob ein Mitarbeiter das Unternehmen verlässt oder nicht.
  • Die Koeffizienten mit einem nicht signifikanten p-Wert (p > 0,05) sind nicht statistisch signifikant und haben keinen signifikanten Einfluss auf das Ergebnis. In diesem Fall ist der Bildungsstand (Master) kein signifikanter Prädiktor.

Vorhersagen treffen

Um Vorhersagen für neue Daten zu treffen, verwenden wir die predict() Funktion:

predictions <- predict(logistic_model, newdata = test, type = "response")

Das newdata Argument gibt die neuen Daten an, für die wir Vorhersagen treffen möchten. Das type Argument gibt den gewünschten Ausgabetyp an. Da wir es mit einer binären Klassifikation zu tun haben, geben wir "response" als Typ an.

Vorhersagen bewerten

Schließlich bewerten wir die Vorhersagen mit der Konfusionsmatrix:

table(Predicted = ifelse(predictions > 0.5, 1, 0), Actual = test$left_company)

Ausgabe:

         Tatsächlich
Vorhergesagt    0    1
        0 1941  334
        1  206  419

Die Verwirrungsmatrix zeigt die Anzahl der wahren Positiven, falschen Positiven, wahren Negativen und falschen Negativen. Mit diesen Werten können wir Leistungsmetriken wie Präzision, Rückruf und F1-Score berechnen.

Schlussfolgerung

In diesem Artikel haben wir die logistische Regressionsgleichung und deren Verwendung zur Modellierung der Beziehung zwischen unabhängigen Variablen und einer abhängigen binären Variablen behandelt. Wir haben auch gezeigt, wie man die glm() Funktion in R verwendet, um ein logistisches Regressionsmodell auf einem Beispieldatensatz zu erstellen, zu trainieren und zu bewerten. Die logistische Regression ist eine leistungsstarke Technik für binäre Klassifikationsprobleme und wird häufig in maschinellem Lernen verwendet.