Skip to content

lab2.dev is launched! Build python web apps with plain English, no code required.

Rにおけるロジスティック回帰方程式：例を用いた式の理解

Rajiv Chandra
Name
Rajiv Chandra

Updated on

ロジスティック回帰は、バイナリ分類問題の機械学習で最も一般的に使用される統計技術の1つです。ロジスティック関数を使用して、従属変数と1つ以上の独立変数（説明変数）の関係をモデル化します。ロジスティック回帰の目的は、入力特徴量と出力変数の最良の関係を見つけることです。この記事では、Rにおけるロジスティック回帰方程式について、例を交えて説明します。

Python Pandas Dataframeからコードなしでデータビジュアライゼーションを素早く作成したいですか？

PyGWalker は、可視化による探索的データ解析のためのPythonライブラリです。 PyGWalker (opens in a new tab) を使うことで、pandas dataframe（および polars dataframe）を Tableau スタイルのユーザーインターフェイスに変換して、ビジュアル的な探索が簡単にできます。

PyGWalker for Data visualization (opens in a new tab)

ロジスティック回帰方程式

ロジスティック回帰方程式は、以下のように定義されます：

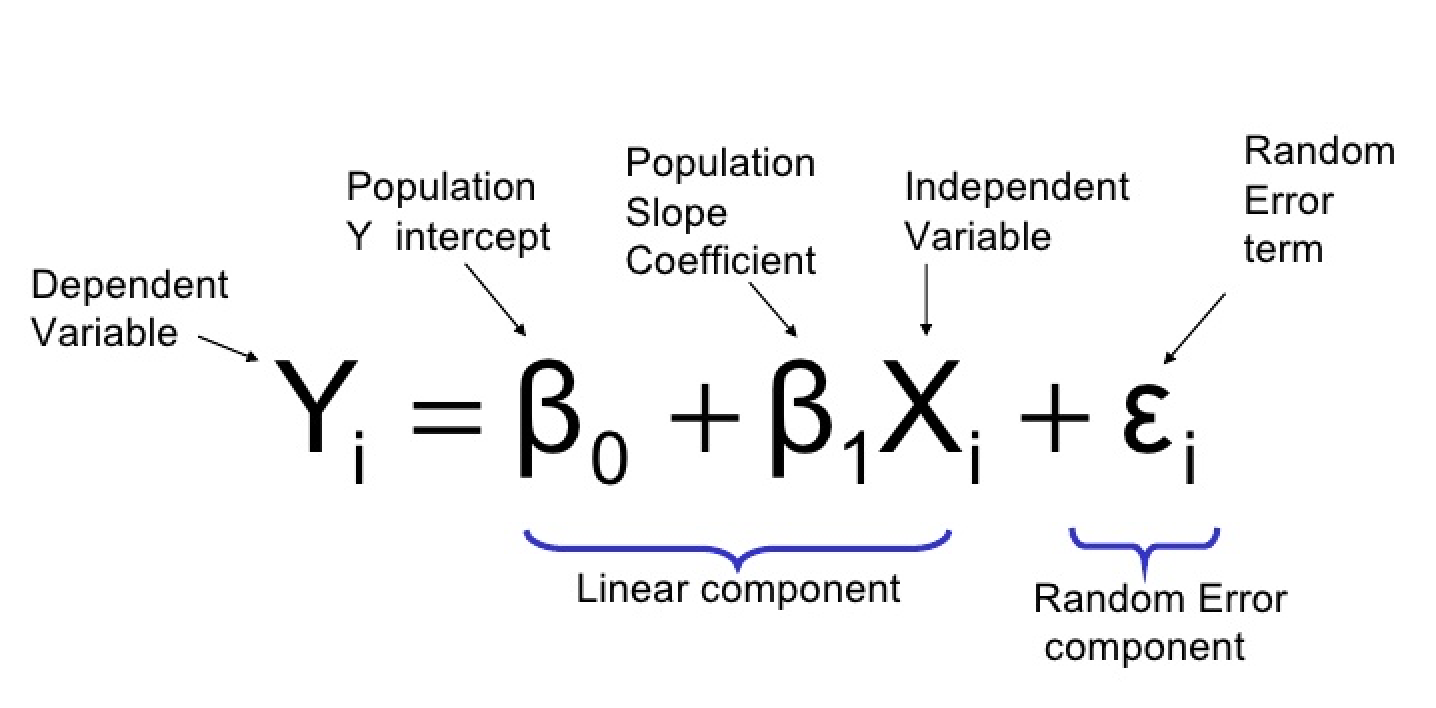
Logistic Regression

ここで：

  • Y：従属変数または反応変数（バイナリ）
  • X1、X2、…、Xp：独立変数または予測変数
  • β0、β1、β2、…、βp：ベータ係数またはモデルパラメータ

ロジスティック回帰モデルは、ベータ係数の値を推定します。ベータ係数は、対応する独立変数が1ユニット変化するときの従属変数の対数オッズの変化を表します。ロジスティック関数（シグモイド関数とも呼ばれる）は、対数オッズを0から1の確率に変換します。

Rにおけるロジスティック回帰の適用

このセクションでは、サンプルデータセットでのロジスティック回帰モデルの構築とトレーニングに、Rのglm（）関数を使用します。RSample パッケージからhr_analyticsデータセットを使用します。

データの読み込み

まず、必要なパッケージとデータセットを読み込みます：

library(RSample)
data(hr_analytics)

hr_analyticsデータセットには、ある企業の従業員に関する情報が含まれており、年齢、性別、学歴、部署、退社したかどうかなどが記録されています。

データの準備

対象変数 left_company をバイナリ変数に変換します：

hr_analytics$left_company <- ifelse(hr_analytics$left_company == "Yes", 1, 0)

次に、データセットをトレーニングセットとテストセットに分割します：

set.seed(123)
split <- initial_split(hr_analytics, prop = 0.7)
train <- training(split)
test <- testing(split)

モデルの作成

glm() 関数を使用してロジスティック回帰モデルを適合します:

logistic_model <- glm(left_company ~ ., data = train, family = "binomial")

この例では利用可能な全ての説明変数 (age, gender, education, department) を使って従属変数 (left_company) を予測するために使われます。family 引数は適合するモデルの種類を指定します。この2値分類問題を扱うため、"binomial"を指定します。

モデルの評価

モデルの性能を評価するために、summary() 関数を使用します:

summary(logistic_model)

出力:

Call:
glm(formula = left_company ~ ., family = "binomial", data = train)

Deviance Residuals: 
   Min      1Q  Median      3Q     Max  
-2.389  -0.640  -0.378   0.665   2.866  

Coefficients:
                     Estimate Std. Error z value Pr(>|z|)    
(Intercept)         -0.721620   0.208390  -3.462 0.000534 ***
age                 -0.008328   0.004781  -1.742 0.081288 .  
genderMale           0.568869   0.086785   6.553 5.89e-11 ***
educationHigh School 0.603068   0.132046   4.567 4.99e-06 ***
educationMaster's   -0.175406   0.156069  -1.123 0.261918    
departmentHR         1.989789   0.171596  11.594  < 2e-16 ***
departmentIT         0.906366   0.141395   6.414 1.39e-10 ***
departmentSales      1.393794   0.177948   7.822 5.12e-15 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 6589.7  on 4799  degrees of freedom
Residual deviance: 5878.5  on 4792  degrees of freedom
AIC: 5894.5

Number of Fisher Scoring iterations: 5

出力はモデルの係数 (beta coefficients)、それらの標準誤差、z値、およびp値を示しています。係数は次のように解釈できます:

  • 有意なp値 (p < 0.05) を持つ係数は統計学的に有意であり、結果に有意な影響を与えます。この例では、年齢、性別、教育、および部署は、従業員が会社を離れるかどうかの有意な予測因子です。
  • 無意味なp値 (p > 0.05) を持つ係数は、統計的に有意ではなく、結果に有意な影響を与えません。この例では、教育レベル（修士）は有意な予測因子ではありません。

予測を行う

新しいデータに対して予測を行うには、predict() 関数を使用します:

predictions <- predict(logistic_model, newdata = test, type = "response")

newdata引数は、予測を行いたい新しいデータを指定します。type引数は、出力タイプを指定します。バイナリ分類を扱っているので、「response」としてタイプを指定します。

予測の評価

最後に、混同行列を使用して予測を評価します。

table(Predicted = ifelse(predictions > 0.5, 1, 0), Actual = test$left_company)

出力:

         Actual
Predicted    0    1
        0 1941  334
        1  206  419

混同行列は、真陽性、偽陽性、真陰性、偽陰性の数を示します。これらの値を使用して、適合率、再現率、F1スコアなどのパフォーマンス指標を計算できます。

結論

この記事では、ロジスティック回帰方程式について説明し、独立変数と従属バイナリ変数の関係をモデル化するために使用される方法について説明しました。また、Rのglm（）関数を使用して、サンプルデータセット上のロジスティック回帰モデルを構築、トレーニング、評価する方法を示しました。ロジスティック回帰は、バイナリ分類問題に対する強力なテクニックであり、機械学習に広く使用されています。