Introduction to K-Means Clustering
Updated on

K-Means is a popular unsupervised learning algorithm used for clustering. It's a centroid-based technique where the aim is to group similar data points together and separate the dissimilar ones. Clustering algorithms are commonly used in machine learning for a variety of applications such as customer profiling, data segmentation, and outlier detection.
What is K-Means Clustering?
K-Means clustering is a method used to partition a data set into K different clusters, where each data point belongs to the cluster with the nearest mean or centroid. It's a way of finding similarities amongst data points in a given data space and grouping them together.
How Does K-Means Clustering Work?
K-Means clustering starts by randomly initializing K centroids. It then assigns each data point to the nearest centroid based on a distance metric, such as the Euclidean Distance. The centroids are recalculated, and the process is repeated until the centroids no longer change significantly or a predefined condition is met.
Advantages and Disadvantages of K-Means Clustering
Advantages
- Simplicity: K-Means is straightforward to understand and implement in Python.
- Efficiency: K-Means is computationally efficient, making it suitable for large data sets.
- Scalability: K-Means can scale to handle large datasets with numerous variables.
Disadvantages
- Number of Clusters: The number of clusters (K) needs to be pre-specified.
- Sensitivity to Initialization: The algorithm's outcome can depend on the initial placement of centroids.
- Outliers: K-Means is sensitive to outliers, which can skew the centroids and the resulting clusters.
Applications of K-Means Clustering
K-Means has a wide array of applications, including:
- Customer Profiling: Companies can use K-Means to segment their customer base and tailor their marketing strategies accordingly.
- Outlier Detection: K-Means can be used to identify anomalies or outliers in datasets, which is important in fields like fraud detection and network security.
- Dimensionality Reduction: K-Means can be used to reduce the dimensionality of data, making it easier to visualize and interpret.
K-Means Clustering Implementation in Python
Python's sklearn library provides a straightforward way to implement K-Means. Here's a basic example:
from sklearn.cluster import KMeans
## Fit the model to the data
kmeans = KMeans(n_clusters=3)
kmeans.fit(data)
## Get the cluster assignments for each data point
labels = kmeans.labels_You can manipulate and preprocess your data using pandas. If you need a refresher on pandas operations, you can check out Modin or PyGWalker (opens in a new tab).
Want to quickly create Data Visualizations in Python?
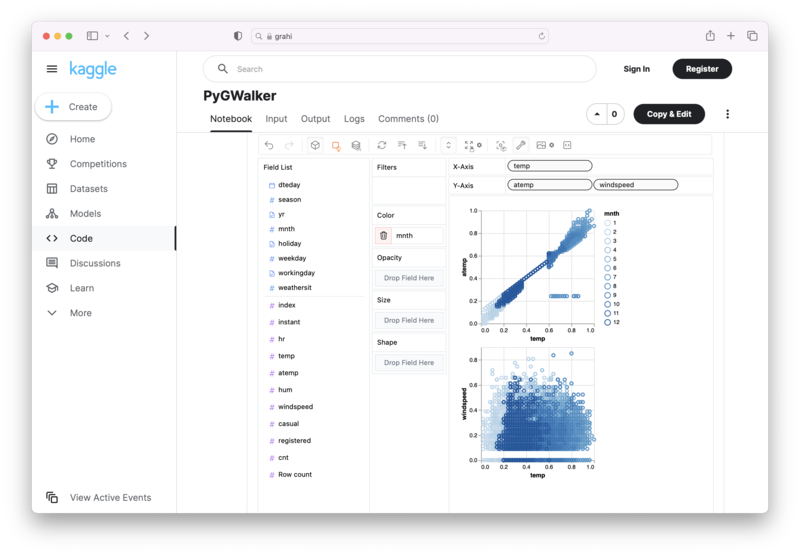
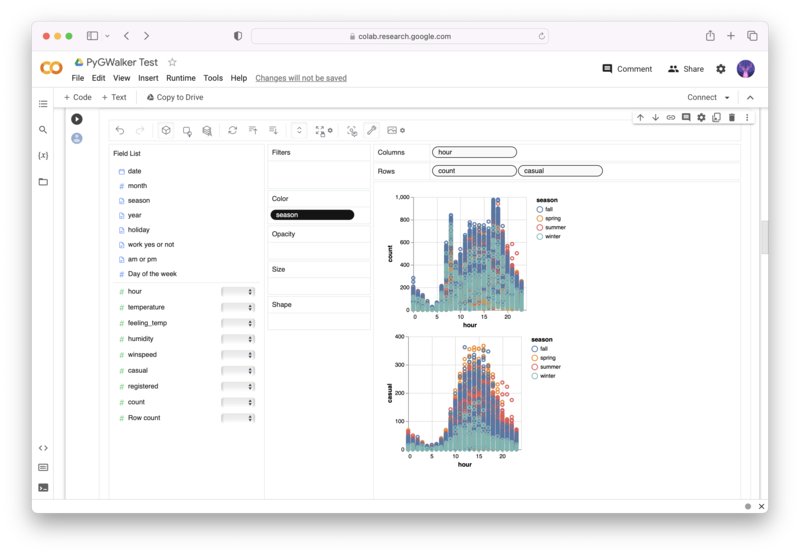
PyGWalker is an Open Source Python Project that can help speed up the data analysis and visualization workflow directly within a Jupyter Notebook-based environments.
PyGWalker (opens in a new tab) turns your Pandas Dataframe (or Polars Dataframe) into a visual UI where you can drag and drop variables to create graphs with ease. Simply use the following code:
pip install pygwalker
import pygwalker as pyg
gwalker = pyg.walk(df)You can run PyGWalker right now with these online notebooks:
And, don't forget to give us a ⭐️ on GitHub!
Clustering Evaluation Metrics
Evaluation metrics help us quantify the quality of our clusters. Here are two commonly used metrics:
- Silhouette Score: Measures how similar an object is to its own cluster compared to other clusters.
- Inertia: Measures the total within-cluster sum of squares. A lower inertia value corresponds to better cluster cohesion.
Comparing K-Means with Other Clustering Algorithms
K-Means vs. Gaussian Mixture Model (GMM)
While both K-Means and the Gaussian Mixture Model (GMM) are clustering algorithms, they have fundamental differences. K-Means is a hard clustering method, meaning a data point belongs entirely to one cluster. In contrast, GMM is a soft clustering method that provides the probability of a data point belonging to each cluster.
K-Means vs. Hierarchical Clustering
K-Means requires specifying the number of clusters upfront, while hierarchical clustering doesn't need this. Hierarchical clustering creates a tree of clusters, which can be visualized and interpreted at different levels, providing more granular information about the data structure.
Use Cases of Clustering
Clustering has numerous use cases in different fields:
- Marketing: For customer segmentation to better understand customer behaviors and tailor marketing strategies.
- Banking: For detecting fraudulent transactions as outliers from the normal behavior.
- Healthcare: For patient segmentation based on their medical history for personalized treatment plans.
Choosing the Number of Clusters
Selecting the right number of clusters is crucial in K-Means. A common method is the Elbow Method, which involves plotting the explained variation as a function of the number of clusters and picking the elbow of the curve as the number of clusters to use.
Outlier Detection using K-Means
K-Means can be used for outlier detection. Data points that are far from the centroid of their assigned cluster can be considered outliers.
Advantages of Unsupervised Learning in Clustering
Unsupervised learning, like clustering, has the advantage of discovering patterns and structures in data without any prior knowledge or training. This makes it particularly useful when we don't have labeled data.
Conclusion
K-Means clustering is a powerful tool in the machine learning toolbox. Its simplicity and versatility make it an excellent choice for tasks ranging from customer segmentation to outlier detection. With a solid understanding of how it works and its potential applications, you're well-equipped to start using K-Means clustering in your own data science projects.