What is the best dimension reduction technique for image data in Python?

While there is no one-size-fits-all answer, PCA is often a great starting point due to its computational efficiency and the fact it captures the directions of maximum variance in the data.

Are there any Python libraries specifically for dimension reduction?

Yes, Python offers several libraries that support various dimension reduction techniques. The most popular one is sklearn, which provides classes for PCA, t-SNE, and many more.

How does dimension reduction benefit machine learning models?

Dimension reduction helps mitigate the curse of dimensionality, thereby improving model performance. It also reduces computational requirements, making it easier to work with large datasets.

Dimension Reduction in Python: Top Tips You Need to Know

Name: Oluwaseun Adeojo

Updated on 8/17/2023

Welcome to the comprehensive guide on dimension reduction in Python. In this data-driven era, the ability to handle high-dimensional datasets has become a non-negotiable skill for every data scientist. It's here that the concept of dimension reduction comes to our rescue, providing a reliable approach to simplify complex, high-dimensional data without losing much information. Our main focus will be on Python – a popular programming language among data science enthusiasts for its simplicity and wide range of data processing libraries.

The ever-increasing volume of data in the contemporary digital world often comes with a high degree of complexity. Such complexity introduces challenges in understanding the underlying structure of the data and hinders effective data modeling and visualization. But worry not, as Python, coupled with powerful dimension reduction techniques, can help us turn this data chaos into meaningful insights.

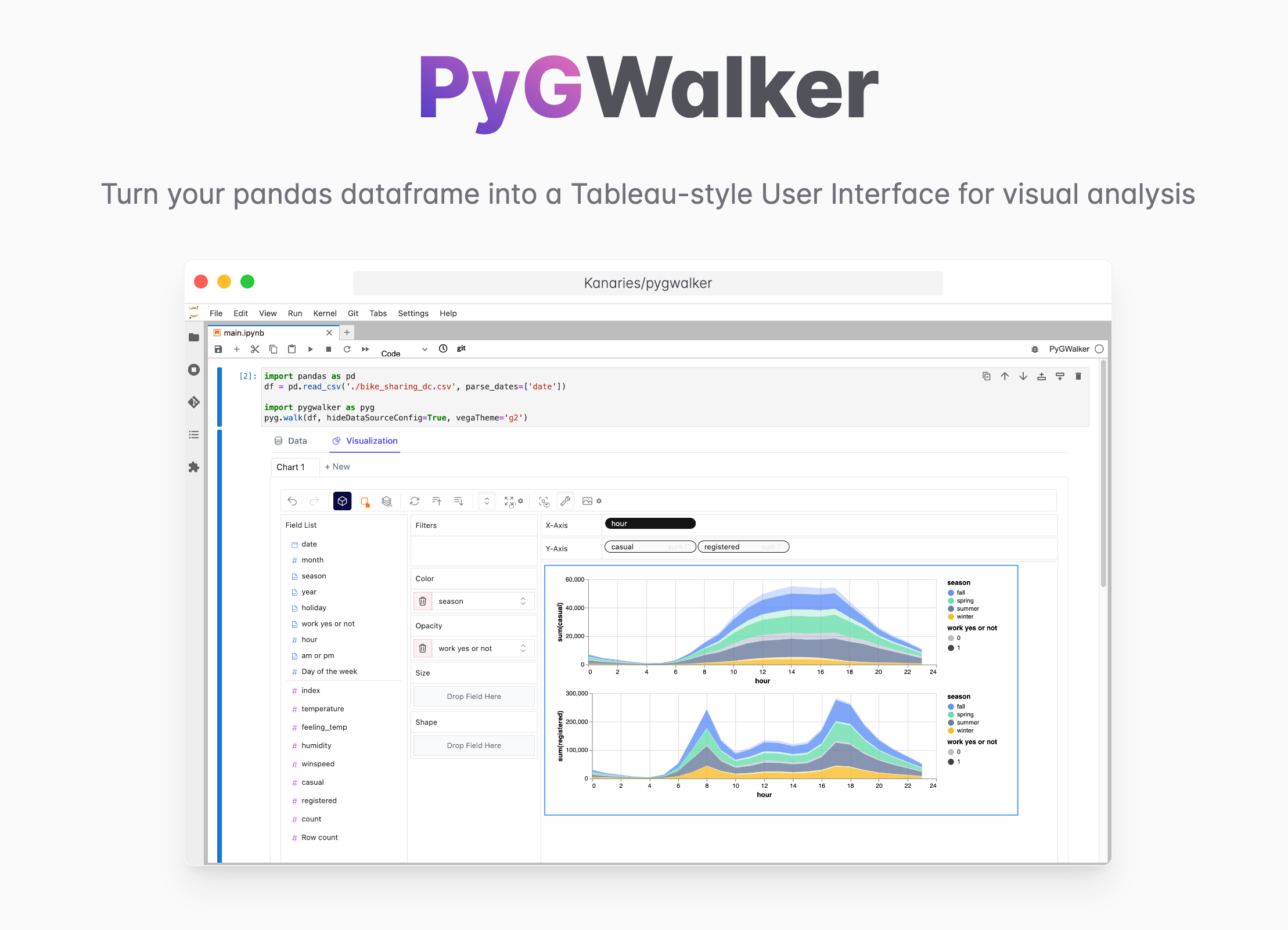
Want to quickly create Data Visualization from Python Pandas Dataframe with No code?

PyGWalker is a Python library for Exploratory Data Analysis with Visualization. PyGWalker (opens in a new tab) can simplify your Jupyter Notebook data analysis and data visualization workflow, by turning your pandas dataframe (and polars dataframe) into a tableau-alternative User Interface for visual exploration.

(opens in a new tab)

Understanding Dimensionality Reduction

Dimensionality reduction, in the realm of machine learning, is the transformation of data from a high-dimensional space into a lower-dimensional space. The objective is to retain as much significant information as possible while eliminating redundancies and noise.

Several dimensionality reduction techniques exist, each with its unique strengths and areas of application. Let's delve into two of the most prevalent ones in Python: Principal Component Analysis (PCA) and t-distributed Stochastic Neighbor Embedding (t-SNE).

Principal Component Analysis (PCA)

PCA is a linear dimensionality reduction technique. It works by identifying the 'principal components' or directions where there is the most variance in the data. The first principal component captures the maximum variance, followed by the second, and so on. In Python, we can leverage the sklearn library to implement PCA.

from sklearn.decomposition import PCA
 
# Assuming X is your high-dimensional dataset
pca = PCA(n_components=2) # We reduce to 2 dimensions
X_reduced = pca.fit_transform(X)

This code block initializes a PCA transformer with two components and applies it to your dataset. The result is a reduced version of the data with most of the original variance preserved.

t-Distributed Stochastic Neighbor Embedding (t-SNE)

Unlike PCA, t-SNE is a nonlinear dimensionality reduction technique. It works on the principle of maintaining the proximity of instances from the high-dimensional space to the low-dimensional space. Python's sklearn library also supports t-SNE implementation.

from sklearn.manifold import TSNE
 
# Assuming X is your high-dimensional dataset
tsne = TSNE(n_components=2, random_state=42) # We reduce to 2 dimensions
X_reduced = tsne.fit_transform(X)

Here, the TSNE object is initialized with two components. The fit_transform function is then used to perform the reduction.

While PCA and t-SNE are powerful tools, they aren't the only ones in our Python arsenal. In our journey through dimension reduction in Python, we will also explore others, including linear discriminant analysis (LDA), kernel PCA, and singular value decomposition (SVD).

Advantages and Disadvantages of Dimensionality Reduction

Like any other technique, dimensionality reduction has its pros and cons. On the one hand, it can drastically reduce the computational cost of modeling, improve model performance by mitigating the curse of dimensionality, and allow for more straightforward data visualization. On the other hand, the reduced dataset may lose interpretability, and important information can sometimes be lost in the process. A deep understanding of these trade-offs is crucial for a data scientist when deciding whether to apply these techniques or not.

Applying Dimension Reduction Techniques to Real-World Problems

The practical application of dimensionality reduction is wide and varied. Below, we'll discuss a few use cases where Python's dimension reduction techniques play a vital role.

Image Processing

High-dimensional data is the norm in image processing, where each pixel can be treated as a feature. Applying dimensionality reduction techniques such as PCA can significantly reduce the complexity of the image data, enabling faster processing and analysis. Let's see a basic example of how PCA can be used for image compression in Python.

from sklearn.decomposition import PCA
from sklearn.datasets import load_sample_image
 
# Load the image
image = load_sample_image('flower.jpg')
 
# Flatten the image
image = image.reshape((image.shape[0], -1))
 
# Apply PCA
pca = PCA(n_components=100)
compressed_image = pca.fit_transform(image)

In the above code, we first flatten the image data. We then apply PCA to reduce the dimensionality of the image data.

Text Data Processing

Text data processing also deals with high-dimensional data, especially when techniques like Bag of Words or TF-IDF are used. Nonlinear dimensionality reduction methods like t-SNE are commonly used in Natural Language Processing (NLP) to visualize high-dimensional text data.

Large Scale Datasets

For massive datasets, dimensionality reduction is almost indispensable. Techniques like PCA can help remove redundant features, speeding up the training process and improving the overall performance of machine learning models.

Now, let's answer a few frequently asked questions about dimension reduction in Python.

FAQ

What is the best dimension reduction technique for image data in Python? While there's no one-size-fits-all answer, PCA is often a great starting point due to its computational efficiency and the fact it captures the directions of maximum variance in the data.
Are there any Python libraries specifically for dimension reduction? Yes, Python offers several libraries that support various dimension reduction techniques. The most popular one is sklearn, which provides classes for PCA, t-SNE, and many more.
How does dimension reduction benefit machine learning models? Dimension reduction helps mitigate the curse of dimensionality, thereby improving model performance. It also reduces computational requirements, making it easier to work with large datasets.

Conclusion

This concludes our first part of the exploration into the world of dimension reduction in Python. The upcoming sections will delve deeper into more advanced dimension reduction techniques, their Python implementations, and practical use-cases.